Registration Using Intenisty Profiles

To test out the registration I began by starting the ring that I am using ten pixels away from the optimal location. Then I implemented the intensity profile metric using the intensities at just one point in the ring. The metric value was calculated by taking the intensities at that point during each step of the registration and finding the least squares error between the model I had created for the intensities when the model was in the optimal location of the image. The preceding movie shows the metric smoothly converging to the correct value since in this case I am using just one point in the model instead of all the points the errors in my model fitting aren't overwhelming the metric value which had been a problem.

To create the model I use a Gaussing plus a Logistic function as illustrated in the following equation

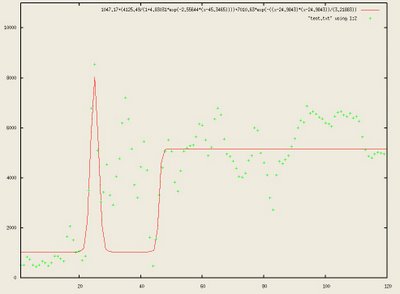
To fit all of the parameters I wrote a C++ program that would find all the peaks by looking at the first derivative using surrounding points and then finding the most significant one by looking at the second derivative. The beginning of the logistic was found using a similar method. To find the rest of the parameters I started out using values roughly in the range of the correct ones and then exhaustively tried different combinations to find the optimal fit. The previous post shows some examples of how well the fit is with some of the data.

When gathering data from the intensities around points from the ring, most conform to the Gaussian-Logistic model except the top and bottom of the ring which is more of two Gaussian functions as illustrated in the following graph

To alleviate this issue the fitting code can be augmented to take into account model selection to see whether a different combinations of Gaussian and logistic functions would work better.

Fitting Intensity Profiles

Using the set up in the receding image, I was able to extract intensities along the red ellipse in the image. I have used a sampling range of 120 pixels to extract data. To accomplish this I implemented the intensity profile class that I had to change slightly to make sure that all the intensities were coming from the outside into the brain so that I could compose a regular model for the data. Once this was done I looked at the graphs of the average intensities that resembled the following graph.

I had initially tried to model the intensities using two Gaussians along with a logistic, but after experimenting with various data I found that some of the data contained up to five Gaussians and some with just one. But usually there was one main Gaussian, so I changed my model to used one Gaussian and one logistic. The following two graphs represent the models that I created in the red color and the data in the green. In some cases I was able to get the model to fit very well in the case of the first graph, but others the match was not as good. I constructed this by making a C++ code that would find the Gaussians by looking at the derivative and second derivative of points to fins it, then I would give a rough estimate for the rest of the parameters in the Gaussian and logistic and many different combinations till I came up with a reasonable one.I also added all the intensity profiles into the registration process where I took a sampling of every tenth face in my ring structure and calculated the intensities of the image at that point compared with the model and then took the least squares error and added it up for each face as the metric value. Right now it seems to be stable if I make the optimizer's movements very minor, but I am not sure whether that is significant.